Matrix Formulation of Bezier Curves
... Or why I thought you might be able to use texture matrices to generate vertices from a Bezier patch control point set. ..Or, why I now think that you can't do that, but why it would be a really good feature to have in DirectX 8, implemented as part of the VertexBuffer interface.

This means that you substitute the paramater value into the row vector u on the left thus for example at point u=0.3 on the bezier curve, we use;
![]()
and then go about pre-multiplying this through the matrix and then post-multiplying the resulting matrix with 1 set of components from the control point vector, P.
This means the if there are 4 control points P0 through P3 then you need to do 3 passes for this calculation. A first pass where the values P0 through P3 are substituted with all the X components of each control point, then the Y’s and then the Z’s.
When using texture matrices in DX7, usually the vertex is given texture components for example tu, tv, tw which might be duplicates of the vertex normal or its position in viewspace coordinates. The result is what is used to lookup values in a typically 2d bitmap;
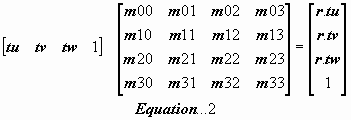
So we would have to jiggle our eqtn1 around to fit this Equation2 format.
We can re-arrange eq1 so that the transpose of the P col vector is pre-multiplied with the transpose of the matrix result of the pre-combination of the row vector U and the basis matrix M.
In symbols;
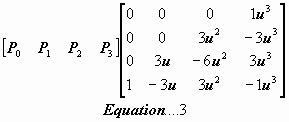
We can store only things which contail spacial data or data that maps to spacial
data. In other words, we can only store information whose components are completely
independent of each other. This means that angular displacements cannot be stored
in the control points, as the interpolation between them would not work as desired.